Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of vertices. A graph may be undirected, meaning that there is no distinction between the two vertices associated with each edge, or its edges may be directed from one vertex to another; see graph (mathematics) for more detailed definitions and for other variations in the types of graphs that are commonly considered. The graphs studied in graph theory should not be confused with graphs of functions or other kinds of graphs.

Graphs are one of the prime objects of study in discrete mathematics. Refer to glossary of graph theory for basic definitions in graph theory.

Applications

Graphs are among the most ubiquitous models of both natural and human-made structures. They can be used to model many types of relations and process dynamics in physical, biological^[1] and social systems. Many problems of practical interest can be represented by graphs.

In computer science, graphs are used to represent networks of communication, data organization, computational devices, the flow of computation, etc. One practical example: The link structure of a website could be represented by a directed graph. The vertices are the web pages available at the website and a directed edge from page A to page B exists if and only if A contains a link to B. A similar approach can be taken to problems in travel, biology, computer chip design, and many other fields. The development of algorithms to handle graphs is therefore of major interest in computer science. There, the transformation of graphs is often formalized and represented by graph rewrite systems. They are either directly used or properties of the rewrite systems (e.g. confluence) are studied. Complementary to graph transformation systems focussing on rule-based in-memory manipulation of graphs are graph databases geared towards transaction-safe, persistent storing and querying of graph-structured data.

Graph-theoretic methods, in various forms, have proven particularly useful in linguistics, since natural language often lends itself well to discrete structure. Traditionally, syntax and compositional semantics follow tree-based structures, whose expressive power lies in the Principle of Compositionality, modeled in a hierarchical graph. Within lexical semantics, especially as applied to computers, modeling word meaning is easier when a given word is understood in terms of related words; semantic networks are therefore important in computational linguistics. Still other methods in phonology (e.g. Optimality Theory, which uses lattice graphs) and morphology (e.g. finite-state morphology, using finite-state transducers) are common in the analysis of language as a graph. Indeed, the usefulness of this area of mathematics to linguistics has borne organizations such as TextGraphs, as well as various 'Net' projects, such as WordNet, VerbNet, and others.

Graph theory is also used to study molecules in chemistry and physics. In condensed matter physics, the three dimensional structure of complicated simulated atomic structures can be studied quantitatively by gathering statistics on graph-theoretic properties related to the topology of the atoms. For example, Franzblau's shortest-path (SP) rings. In chemistry a graph makes a natural model for a molecule, where vertices represent atoms and edges bonds. This approach is especially used in computer processing of molecular structures, ranging from chemical editors to database searching. In statistical physics, graphs can represent local connections between interacting parts of a system, as well as the dynamics of a physical process on such systems.

Graph theory is also widely used in sociology as a way, for example, to measure actors' prestige or to explore diffusion mechanisms, notably through the use of social network analysis software.

Likewise, graph theory is useful in biology and conservation efforts where a vertex can represent regions where certain species exist (or habitats) and the edges represent migration paths, or movement between the regions. This information is important when looking at breeding patterns or tracking the spread of disease, parasites or how changes to the movement can affect other species.

In mathematics, graphs are useful in geometry and certain parts of topology, e.g. Knot Theory. Algebraic graph theory has close links with group theory.

A graph structure can be extended by assigning a weight to each edge of the graph. Graphs with weights, or weighted graphs, are used to represent structures in which pairwise connections have some numerical values. For example if a graph represents a road network, the weights could represent the length of each road.

A digraph with weighted edges in the context of graph theory is called a network. Network analysis have many practical applications, for example, to model and analyze traffic networks. Applications of network analysis split broadly into three categories:

First, analysis to determine structural properties of a network, such as the distribution of vertex degrees and the diameter of the graph. A vast number of graph measures exist, and the production of useful ones for various domains remains an active area of research.
Second, analysis to find a measurable quantity within the network, for example, for a transportation network, the level of vehicular flow within any portion of it.
Third, analysis of dynamical properties of networks.

History

The first text book on graph theory was written by Denes Konig, but this book was very hard to understand. Richard Rado said he was unable to understand Konig's proof of Rado's Theorem. The first readable book was by Frank Harary and was enormously popular. This book enabled mathematicians, chemists, electrical engineers and social scientists to talk to each other. He donated all of the proceeds to fund the Polya Prize.

The paper written by Leonhard Euler on the Seven Bridges of Königsberg and published in 1736 is regarded as the first paper in the history of graph theory.^[2] This paper, as well as the one written by Vandermonde on the knight problem, carried on with the analysis situs initiated by Leibniz. Euler's formula relating the number of edges, vertices, and faces of a convex polyhedron was studied and generalized by Cauchy^[3] and L'Huillier,^[4] and is at the origin of topology.

More than one century after Euler's paper on the bridges of Königsberg and while Listing introduced topology, Cayley was led by the study of particular analytical forms arising from differential calculus to study a particular class of graphs, the trees. This study had many implications in theoretical chemistry. The involved techniques mainly concerned the enumeration of graphs having particular properties. Enumerative graph theory then rose from the results of Cayley and the fundamental results published by Pólya between 1935 and 1937 and the generalization of these by De Bruijn in 1959. Cayley linked his results on trees with the contemporary studies of chemical composition.^[5] The fusion of the ideas coming from mathematics with those coming from chemistry is at the origin of a part of the standard terminology of graph theory.

In particular, the term "graph" was introduced by Sylvester in a paper published in 1878 in Nature, where he draws an analogy between "quantic invariants" and "co-variants" of algebra and molecular diagrams:^[6]

"[...] Every invariant and co-variant thus becomes expressible by a graph precisely identical with a Kekuléan diagram or chemicograph. [...] I give a rule for the geometrical multiplication of graphs, i.e. for constructing a graph to the product of in- or co-variants whose separate graphs are given. [...]" (italics as in the original).

One of the most famous and productive problems of graph theory is the four color problem: "Is it true that any map drawn in the plane may have its regions colored with four colors, in such a way that any two regions having a common border have different colors?" This problem was first posed by Francis Guthrie in 1852 and its first written record is in a letter of De Morgan addressed to Hamilton the same year. Many incorrect proofs have been proposed, including those by Cayley, Kempe, and others. The study and the generalization of this problem by Tait, Heawood, Ramsey and Hadwiger led to the study of the colorings of the graphs embedded on surfaces with arbitrary genus. Tait's reformulation generated a new class of problems, the factorization problems, particularly studied by Petersen and Kőnig. The works of Ramsey on colorations and more specially the results obtained by Turán in 1941 was at the origin of another branch of graph theory, extremal graph theory.

The four color problem remained unsolved for more than a century. In 1969 Heinrich Heesch published a method for solving the problem using computers.^[7] A computer-aided proof produced in 1976 by Kenneth Appel and Wolfgang Haken makes fundamental use of the notion of "discharging" developed by Heesch.^[8]^[9] The proof involved checking the properties of 1,936 configurations by computer, and was not fully accepted at the time due to its complexity. A simpler proof considering only 633 configurations was given twenty years later by Robertson, Seymour, Sanders and Thomas.^[10]

The autonomous development of topology from 1860 and 1930 fertilized graph theory back through the works of Jordan, Kuratowski and Whitney. Another important factor of common development of graph theory and topology came from the use of the techniques of modern algebra. The first example of such a use comes from the work of the physicist Gustav Kirchhoff, who published in 1845 his Kirchhoff's circuit laws for calculating the voltage and current in electric circuits.

The introduction of probabilistic methods in graph theory, especially in the study of Erdős and Rényi of the asymptotic probability of graph connectivity, gave rise to yet another branch, known as random graph theory, which has been a fruitful source of graph-theoretic results.

Drawing graphs

Main article: Graph drawing

Graphs are represented graphically by drawing a dot or circle for every vertex, and drawing an arc between two vertices if they are connected by an edge. If the graph is directed, the direction is indicated by drawing an arrow.

A graph drawing should not be confused with the graph itself (the abstract, non-visual structure) as there are several ways to structure the graph drawing. All that matters is which vertices are connected to which others by how many edges and not the exact layout. In practice it is often difficult to decide if two drawings represent the same graph. Depending on the problem domain some layouts may be better suited and easier to understand than others.

Graph-theoretic data structures

Main article: Graph (data structure)

There are different ways to store graphs in a computer system. The data structure used depends on both the graph structure and the algorithm used for manipulating the graph. Theoretically one can distinguish between list and matrix structures but in concrete applications the best structure is often a combination of both. List structures are often preferred for sparse graphs as they have smaller memory requirements. Matrix structures on the other hand provide faster access for some applications but can consume huge amounts of memory.

List structures

Incidence list: The edges are represented by an array containing pairs (tuples if directed) of vertices (that the edge connects) and possibly weight and other data. Vertices connected by an edge are said to be adjacent.
Adjacency list: Much like the incidence list, each vertex has a list of which vertices it is adjacent to. This causes redundancy in an undirected graph: for example, if vertices A and B are adjacent, A's adjacency list contains B, while B's list contains A. Adjacency queries are faster, at the cost of extra storage space.

Matrix structures

Incidence matrix: The graph is represented by a matrix of size |V | (number of vertices) by |E| (number of edges) where the entry [vertex, edge] contains the edge's endpoint data (simplest case: 1 - incident, 0 - not incident).
Adjacency matrix: This is an n by n matrix A, where n is the number of vertices in the graph. If there is an edge from a vertex x to a vertex y, then the element 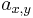$a_{x, y}$ is 1 (or in general the number of xy edges), otherwise it is 0. In computing, this matrix makes it easy to find subgraphs, and to reverse a directed graph.
Laplacian matrix or "Kirchhoff matrix" or "Admittance matrix": This is defined as D − A, where D is the diagonal degree matrix. It explicitly contains both adjacency information and degree information. (However, there are other, similar matrices that are also called "Laplacian matrices" of a graph.)
Distance matrix: A symmetric n by n matrix D, where n is the number of vertices in the graph. The element 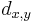$d_{x, y}$ is the length of a shortest path between x and y; if there is no such path 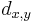$d_{x, y}$ = infinity. It can be derived from powers of A; $d_{x,y}=\min\{n\mid A^n[x,y]\ne 0\}. \,$

Problems in graph theory

Enumeration

There is a large literature on graphical enumeration: the problem of counting graphs meeting specified conditions. Some of this work is found in Harary and Palmer (1973).

Subgraphs, induced subgraphs, and minors

A common problem, called the subgraph isomorphism problem, is finding a fixed graph as a subgraph in a given graph. One reason to be interested in such a question is that many graph properties are hereditary for subgraphs, which means that a graph has the property if and only if all subgraphs have it too. Unfortunately, finding maximal subgraphs of a certain kind is often an NP-complete problem.

Finding the largest complete graph is called the clique problem (NP-complete).

A similar problem is finding induced subgraphs in a given graph. Again, some important graph properties are hereditary with respect to induced subgraphs, which means that a graph has a property if and only if all induced subgraphs also have it. Finding maximal induced subgraphs of a certain kind is also often NP-complete. For example,

Finding the largest edgeless induced subgraph, or independent set, called the independent set problem (NP-complete).

Still another such problem, the minor containment problem, is to find a fixed graph as a minor of a given graph. A minor or subcontraction of a graph is any graph obtained by taking a subgraph and contracting some (or no) edges. Many graph properties are hereditary for minors, which means that a graph has a property if and only if all minors have it too. A famous example:

A graph is planar if it contains as a minor neither the complete bipartite graph 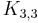$K_{3,3}$ (See the Three-cottage problem) nor the complete graph $K_{5}$ .

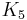Another class of problems has to do with the extent to which various species and generalizations of graphs are determined by their point-deleted subgraphs, for example:

The reconstruction conjecture.

Graph coloring

Many problems have to do with various ways of coloring graphs, for example:

The four-color theorem
The strong perfect graph theorem
The Erdős–Faber–Lovász conjecture (unsolved)
The total coloring conjecture (unsolved)
The list coloring conjecture (unsolved)
The Hadwiger conjecture (graph theory) (unsolved).

Route problems

Hamiltonian path and cycle problems
Minimum spanning tree
Route inspection problem (also called the "Chinese Postman Problem")
Seven Bridges of Königsberg
Shortest path problem
Steiner tree
Three-cottage problem
Traveling salesman problem (NP-hard)

Network flow

There are numerous problems arising especially from applications that have to do with various notions of flows in networks, for example:

Max flow min cut theorem

Visibility graph problems

Museum guard problem

Covering problems

Covering problems are specific instances of subgraph-finding problems, and they tend to be closely related to the clique problem or the independent set problem.

Graph classes

Many problems involve characterizing the members of various classes of graphs. Overlapping significantly with other types in this list, this type of problem includes, for instance:

Enumerating the members of a class
Characterizing a class in terms of forbidden substructures
Ascertaining relationships among classes (e.g., does one property of graphs imply another)
Finding efficient algorithms to decide membership in a class
Finding representations for members of a class.

Notes

^ Mashaghi, A.; et al. (2004). "Investigation of a protein complex network". European Physical Journal B 41 (1): 113–121. doi:10.1140/epjb/e2004-00301-0.
^ Biggs, N.; Lloyd, E. and Wilson, R. (1986), Graph Theory, 1736-1936, Oxford University Press
^ Cauchy, A.L. (1813), "Recherche sur les polyèdres - premier mémoire", Journal de l'Ecole Polytechnique 9 (Cahier 16): 66–86.
^ L'Huillier, S.-A.-J. (1861), "Mémoire sur la polyèdrométrie", Annales de Mathématiques 3: 169–189.
^ Cayley, A. (1875), "Ueber die Analytischen Figuren, welche in der Mathematik Bäume genannt werden und ihre Anwendung auf die Theorie chemischer Verbindungen", Berichte der deutschen Chemischen Gesellschaft 8 (2): 1056–1059, doi:10.1002/cber.18750080252.
^ John Joseph Sylvester (1878), Chemistry and Algebra. Nature, volume 17, page 284. doi:10.1038/017284a0. Online version. Retrieved 2009-12-30.
^ Heinrich Heesch: Untersuchungen zum Vierfarbenproblem. Mannheim: Bibliographisches Institut 1969.
^ Appel, K. and Haken, W. (1977), "Every planar map is four colorable. Part I. Discharging", Illinois J. Math. 21: 429–490.
^ Appel, K. and Haken, W. (1977), "Every planar map is four colorable. Part II. Reducibility", Illinois J. Math. 21: 491–567.
^ Robertson, N.; Sanders, D.; Seymour, P. and Thomas, R. (1997), "The four color theorem", Journal of Combinatorial Theory Series B 70: 2–44, doi:10.1006/jctb.1997.1750.

References

Berge, Claude (1958), Théorie des graphes et ses applications, Collection Universitaire de Mathématiques, II, Paris: Dunod . English edition, Wiley 1961; Methuen & Co, New York 1962; Russian, Moscow 1961; Spanish, Mexico 1962; Roumanian, Bucharest 1969; Chinese, Shanghai 1963; Second printing of the 1962 first English edition, Dover, New York 2001.
Biggs, N.; Lloyd, E.; Wilson, R. (1986), Graph Theory, 1736–1936, Oxford University Press .
Bondy, J.A.; Murty, U.S.R. (2008), Graph Theory, Springer, ISBN 978-1-84628-969-9 .
Bondy, Riordan, O.M (2003), Mathematical results on scale-free random graphs in "Handbook of Graphs and Networks" (S. Bornholdt and H.G. Schuster (eds)), Wiley VCH, Weinheim, 1st ed. .
Chartrand, Gary (1985), Introductory Graph Theory, Dover, ISBN 0-486-24775-9 .
Gibbons, Alan (1985), Algorithmic Graph Theory, Cambridge University Press .
Reuven Cohen, Shlomo Havlin (2010), Complex Networks: Structure, Robustness and Function, Cambridge University Press
Golumbic, Martin (1980), Algorithmic Graph Theory and Perfect Graphs, Academic Press .
Harary, Frank (1969), Graph Theory, Reading, MA: Addison-Wesley .
Harary, Frank; Palmer, Edgar M. (1973), Graphical Enumeration, New York, NY: Academic Press .
Mahadev, N.V.R.; Peled, Uri N. (1995), Threshold Graphs and Related Topics, North-Holland .
Mark Newman (2010), Networks: An Introduction, Oxford University Press .

External links

Online textbooks

Graph Theory with Applications (1976) by Bondy and Murty
Phase Transitions in Combinatorial Optimization Problems, Section 3: Introduction to Graphs (2006) by Hartmann and Weigt
Digraphs: Theory Algorithms and Applications 2007 by Jorgen Bang-Jensen and Gregory Gutin
Graph Theory, by Reinhard Diestel

Other resources

Graph theory tutorial
A searchable database of small connected graphs
Image gallery: graphs
Concise, annotated list of graph theory resources for researchers
rocs - a graph theory IDE

Areas of mathematics

Areas	Arithmetic · Algebra (elementary – linear – multilinear – abstract) · Geometry (Discrete geometry – Algebraic geometry – Differential geometry) · Calculus/Analysis · Set theory · Logic · Category theory · Number theory · Combinatorics · Graph theory · Topology · Lie theory · Differential equations/Dynamical systems · Mathematical physics · Numerical analysis · Computation · Information theory · Probability · Statistics · Optimization · Control theory · Game theory

Divisions	Pure mathematics · Applied mathematics · Discrete mathematics · Computational mathematics

Category · Mathematics portal · Outline · Lists